УДК 631.3
ГРНТИ 55.57.31
Экспериментальный мониторинг упругих стоек культиватора
Бутовченко А.В., Игнотенко И.В., Рулевский А.М.
Донской государственный технический университет, г. Ростов-на-Дону, РФ
В полевых условиях применение специальных стендов затруднено, поэтому для оперативного контроля целесообразно применять обобщенный метод по трем нагружениям.
Этот метод основывается на возможности определения девяти неизвестных коэффициентов 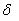
||SM|| = ||∆||x||PM|| (4.1)
где ||SM||,||PM|| составлены из векторов-столбцов соответственно трех смещений Sj и трех нагрузок Pj .(j=1.2,3). Таким образом» матрица податливости определяемая соотношением:
||∆|| = ||SM||x||PM||-1 (4.2)
Чтобы решение не вырождалось (detP≠0), уравнения не должны быть линейной комбинацией друг друга, т.е., прикладываемые вектора силы не должны быть параллельны.
Матрица угловых искажений Н может также определяться по трем нагрузкам P1,P2,P3. Имеем три основных соотношения:
Объединяя их в одно матичное уравнение получаем:
||ⱷM|| = ||H||x||PM|| (4.3)
где матрица углов поворота ||ⱷМ|| составлена из векторов-столбцов ⱷj. Отсюда:
||H|| = ||ⱷM||x||PM||-1 (4.4)
Расчеты по предложенным зависимостям можно выполнять на ЭВМ,
применяя стандартные подпрограммы, матричной алгебры. Однако измерение всех этих составляющих производится вручную и представляет трудоемкую задачу. Кроме того, применение визуальных методов измерения не дает достаточную точность.
В итоге алгоритм определения упругих свойств крепления рабочего органа по трем изменениям будет заключаться в следующем :
1. Координаты начального положения трех точек A, B, С рабочего органа в виде вектора:
s0 = {xА, zА, yА, xВ, zВ, yВ, xС, zС, yС}T
нагрузку P1 = {P1 P1 P1}T,
координаты положения трех точек A, B, С :
s1 = { xА, zА, yА, xВ, zВ, yВ, xС, zС, yС }T;
нагрузку P1 = {P1 P1 P1}T,
координаты смещений трех точек A, B, С :
s2 = { xА, zА, yА, xВ, zВ, yВ, xС, zС, yС }T;
нагрузку P1 = {P1 P1 P1}T,
координаты смещений трех точек A, B, С :
s3 = { xА, zА, yА, xВ, zВ, yВ, xС, zС, yС }T.
2. Формирование матрицы
[PM] =
3.Формирование вектор-столбцов
sAJ = 
4.Формирование матрицы [sM] смещений носка рабочего органа - т.А. [sM] = { sA1, sA2, sA3 } .
5.Обращение матрицы [PM]
[PM] = [PM]-1
6.Определяем матрицу податливости [D] перемножением матриц (строки на столбцы) [D] = [sM] [PM].
Должно соблюдаться равенство
Dik = Dki .
7.Определение матрицы жесткости
[C] = [D]-1
8.Определяем массив начальных углов ориентации рабочего органа X0 размерности 3:
X01 = arctg {(z E– zB) / (yE – yB)}
X02 = arctg {( yE – yA) / (xE – xA)}
X01 = arctg {(z E– zA) / (xE – xA)}
где xE = (xВ + xС)/2 zE = (zВ + zС)/2 уE = (уВ + уС)/2 – средние значения.
9.Определяем массив углов ориентации рабочего органа для каждого нагружения
XJ1 = arctg {(sJ8– sJ5) / (sJ9– sJ6)} , J = 1, 2, 3;
XJ1 = arctg {(sJ9– sJ3) / (sJ7– sJ1)} , J = 1, 2, 3;
XJ1 = arctg {(sJ8– sJ2) / (sJ7– sJ1)} , J = 1, 2, 3.
10.Определяем углы поворота jJ отнонию к начальному положению
jJ = XJ - X0 , J = 1, 2, 3.
II.Формирование матрицы [jM]
[jM] = {j1, j2, j3}
12.Вычисляем матрицы угловых искажений [H] перемножением матриц:
[H] = [jM] [PM]-1
13.Должно выполняться условие
[jM] (I, I) =0 , I = 1, 2, 3.
14.Печать значений [D], [C], [H] .
5. Экспериментальные исследования и анализ их результатов
Эксперимент заключается в следующем, на нагрузочный стенд крепится стойка с лапой. Прикладывается нагрузка в горизонтальном направлении, ступень нагружения 20 кг. Замеряются координаты трех точек, и сводятся в таблицу. По полученным данным строится траектория смещения носка рабочего органа, и определяется номинальная нагрузка. Затем прикладывается нагрузка еще по двум направлениям с замерами координат.
По полученным данным производится расчет в программе excel.
Были проведены испытания пяти разных стоек. Ниже представлены описание этих стоек, таблицы координат положения трех точек лапы, и расчета матрицы жесткости, так же представлены графики определения траектории смещения носка лапы под нагрузкой, график силовой характеристики, и тангаж лапы.
Геометрические размеры стоек и подвесок приведены в таблице 1.
Таблица 1
|
Номер стойки |
Ширина захвата лапы, мм |
Высота крепления, Н, мм |
Отнесение носка Т, мм |
Сечение упругого элемента, мм×мм |
Рабочая нагрузка, кН |
Масса, кг |
Удельная метал- лоёмкость, кг/кН |
|
1 |
65 |
650 |
270 |
40×40 |
2,0 |
22,5 |
11,25 |
|
2 |
330 |
450 |
30 |
42×20 |
1,0 |
10,4 |
10,4 |
|
3 |
270 |
460 |
–70 |
30×10×2 |
0,8 |
5,2 |
6,5 |
|
4 |
400 |
750 |
80 |
50×25 |
1,7 |
32,0 |
18,8 |
|
5 |
330 |
450 |
150 |
40×20 |
1,0 |
16,3 |
16,3 |
Предохранительная подвеска лапы культиваторов КПКсо спиральной нажимной пружиной изображена на рисунке 4
Рисунок 10. Подвеска лапы культиваторов КПК
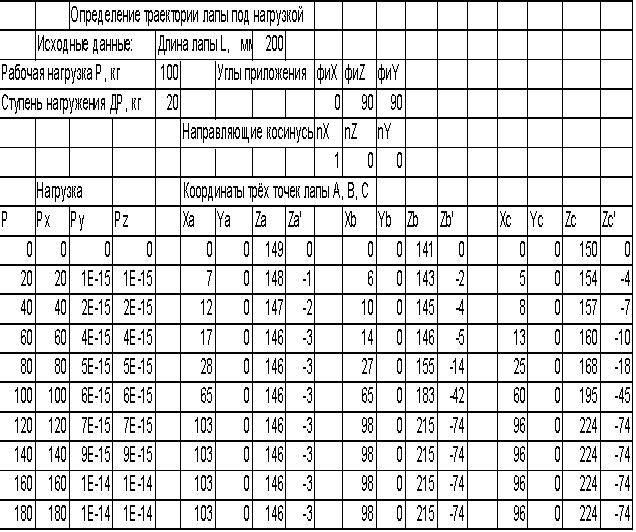
Координаты начального положения трех точек A, B, С рабочего органа под различной нагрузкой и угол поворота лапы представлены в таблице 2.
Таблица 2-Координаты трех точек лапы
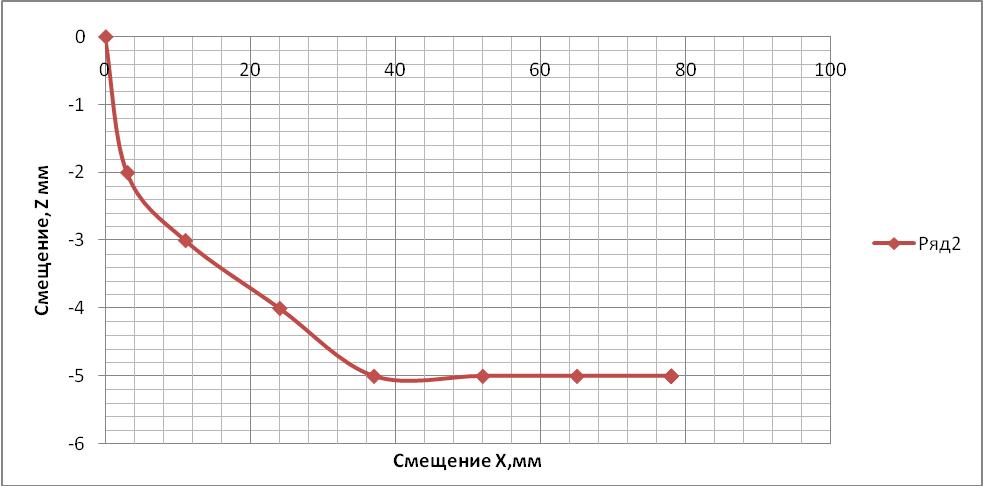
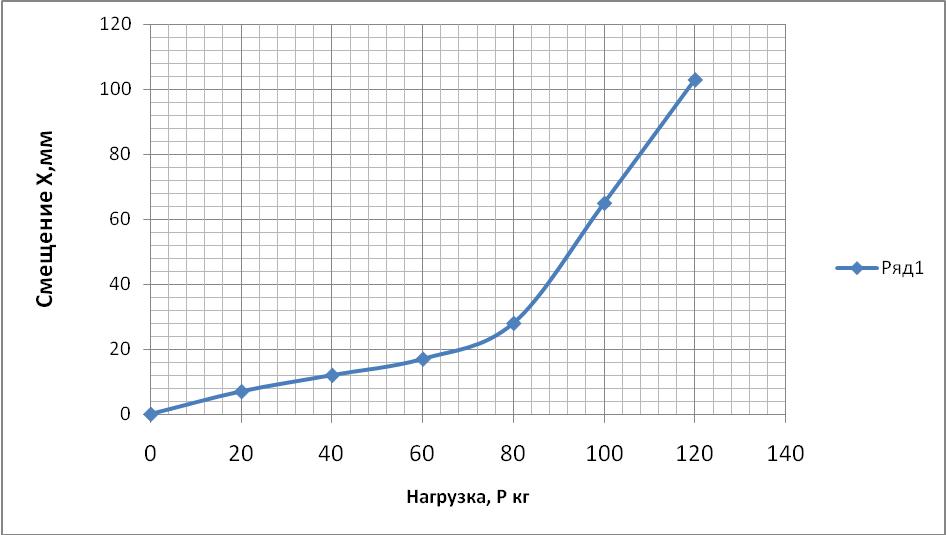
по данным таблицы 2 построена диаграмма (рисунок 11) на которой показана траектория смещения носка лапы. По этой траектории определена рабочая нагрузка. На графике видно, что от нуля до сорока мм идет заглубление, а от сорока и до восьмидесяти смещение не меняется, в этом пределе находится рабочая нагрузка.
Рисунок 11 Траектория носка лапы под нагрузкой
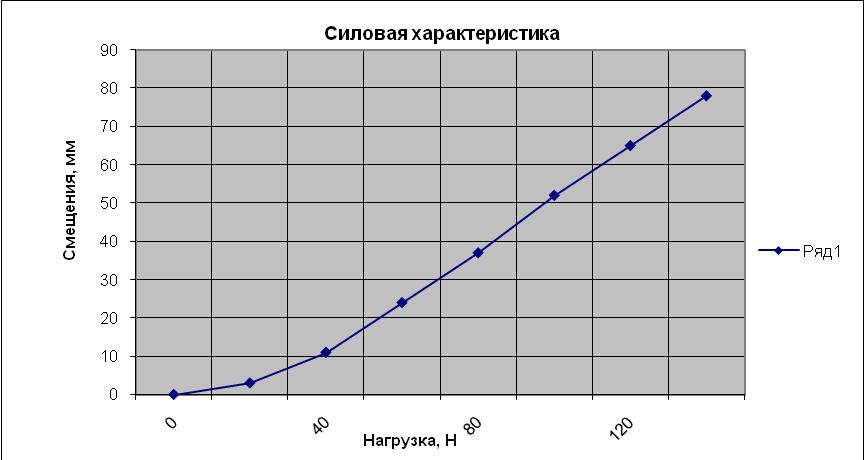
На рисунке 12 изображена график силовой характеристики. Он показывает смещение носка лапы относительно приложенной нагрузки. На нем видно, что с увеличением нагрузки увеличивается смещение. Максимальным смещение является при нагрузке в 140 кг.
Рисунок 12 Силовая характеристика
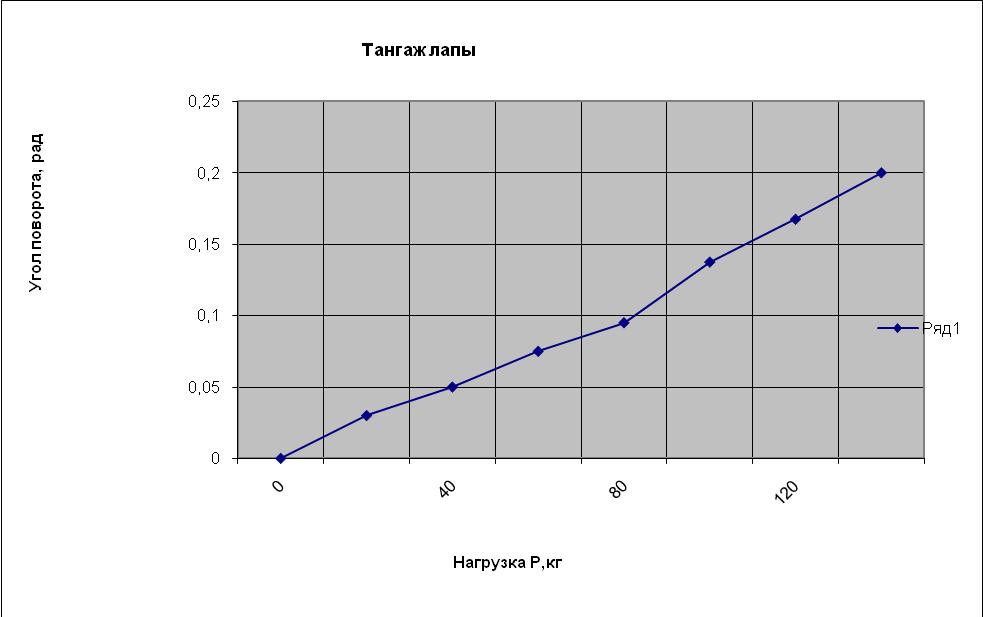
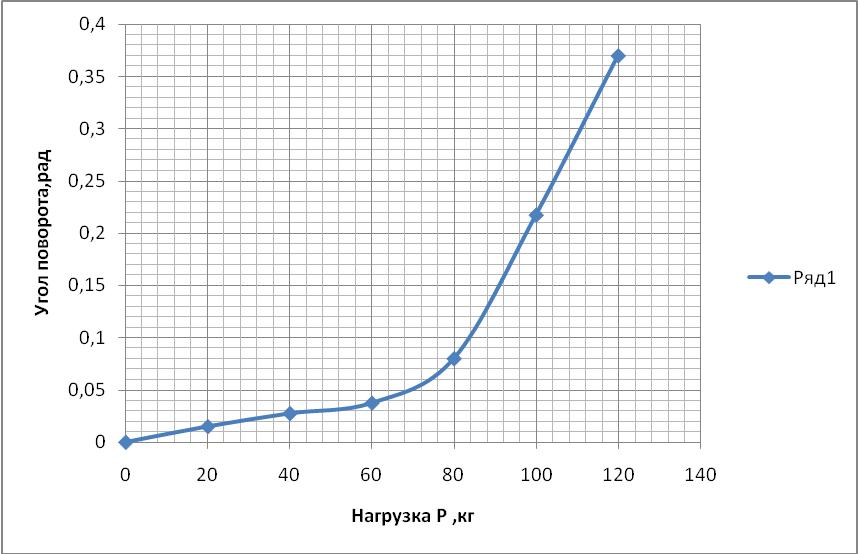
Изменение угла поворота лапы в зависимости от нагрузки показано на рисунке 13. На графике видно, что с увеличением нагрузки увеличивается угол поворота лапы. Максимальное значение угол поворота имеет при нагрузке в 130 кг.
Рисунок 13 Тангаж лапы
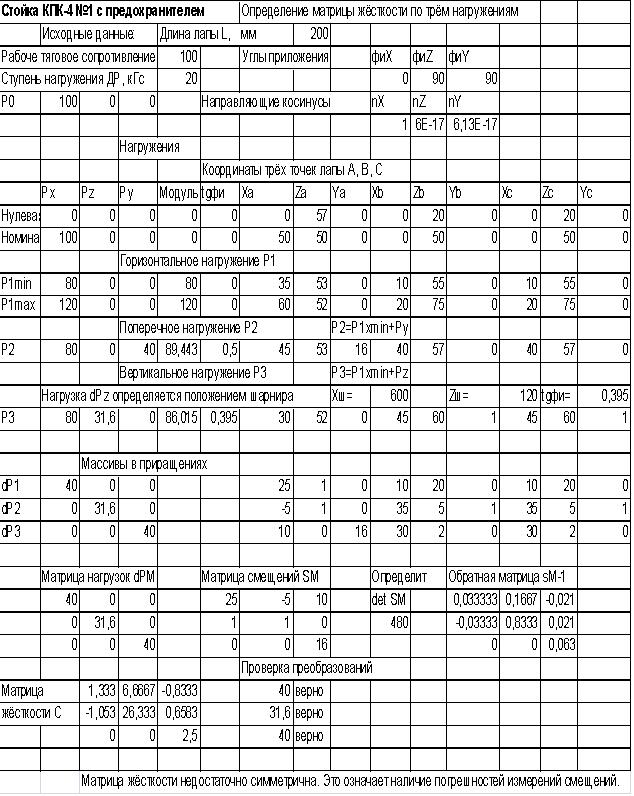
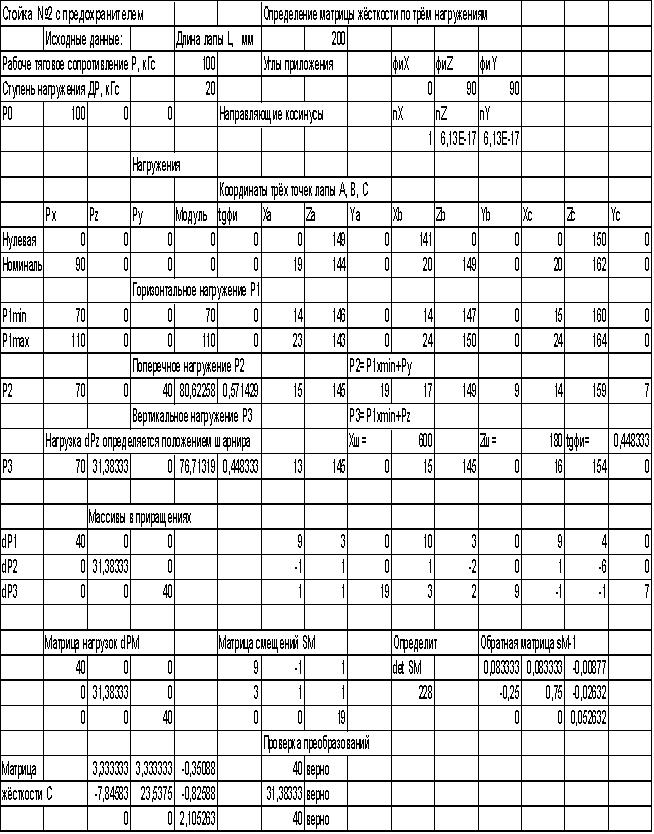
В расчетной таблице 3, представлены исходные данные стойки КПК-4, нагрузки, и координаты трех точек лапы. Рассчитана матрица жесткости.
Таблица 3.-Расчетная таблица для стойки КПК-4
Стойка (рис 5) (ГОСТдугообразная пружинная стойка, предназначенная для плоскорежущих лап В = 410.
Рисунок 14. Стойка 13 (ГОСТ 23.2.164—87)
Координаты трех точек лапы стойки 13, ступень нагружения, направляющие косинусы и нагрузка представлены в таблице 4.
Таблица 4. Координаты трех точек лапы стойки 13
На рисунке 15 показан график определения траектории смещения носка лапы. По данной траектории определяется рабочая нагрузка. Она находится в пределах от сорока до шестидесяти, так как в этом пределе смещения по z, не происходит.
Рисунок 15 Траектория носка лапы под нагрузкой стойка 13
Силовая характеристика стойки 13 оказана на рисунке 16 в пределах приложения нагрузки от нуля до восьмидесяти килограмм, смещение носка лапы изменяется примерно одинаково, а в пределе от восьмидесяти до ста двадцати килограмм, происходит резкий скачок смещения.
Рисунок 16- Силовая характеристика стойки 13
На графике угла поворота лапы (рис.17), видно что от 0 до 80 килограмм угол меняется незначительно до -0.1 рад, а в пределе от 80 до 120 происходит резкий скачек и величина угла доходит до -0,4 рад.
Рисунок 17. Угол поворота лапы
В расчетной таблице 5, представлены исходные данные стойки 13, прилагаемые нагрузки, и координаты трех точек лапы. Рассчитана матрица жесткости. По расчетам можно сделать вывод о том:
Таблица 5-Расчетная таблица для стойки 13
6. Методика обработки результатов
Обработка результатов проводилась в программе Excel. Определение матрицы жесткости по трем направлениям.
Вначале в таблицу заносим исходные данные:
Рабочее тяговое сопротивление Р, кГс(Е3); Ступень нагружения Р1, кГс(Е4), длина лапы мм(Н2); углы приложения (J4; K4; L4).
Затем вносим значения координат трех точек лапы А, В, С при нулевой(B10) и номинальной(B11) нагрузке.
Координаты при нулевой нагрузке (G10; H10; I10; J10; K10; L10; M10; N10; O11).
Координаты при номинальной нагрузке (G11;H11;I11;J11;K11;L11;M11;N11;O11).
Для горизонтального нагружения P1: Определяем минимальную(B13) и максимальную(B14) нагрузку Р1min (=B11-E4); P1max=(=B11+E4); и заносим значения координат трех точек лапы при P1min и P1max.
КоординатыP1min(G13;H13;I13;J13;K13;L13;M13;N13;O13)
КоординатыP1max(G14;H14;I14;J14;K14;L14;M14;N14;O14)
Для поперечного нагружения P2: выбираем минимальную нагрузку P1min(B13), далее определяем модуль(Е16) (=КОРЕНЬ(B16^2+D16^2)) и угол tgф(F16)(=D16/B16) после заносим данные о координатах трех точек лапы.
Координаты: (G16;H16;I16;J16;K16;L16;M16;N16;O16).
Для вертикального нагружения Р3: выбираем минимальную нагрузку P1min(B13), определяем вертикальную нагрузку Pz(=B19*O18), определяем модуль (=КОРЕНЬ(B19^2+C19^2)) и угол tgф(=(H10+300-M18)/(J18-G10)), далее заносим координаты трех точек лапы.
Координаты (G19;H19;I19;J19;K19;L19;M19;N19;O19).
Далее по полученным данным нагрузки в трех положениях и координат точек лапы составляем матрицы:
Составляем матрицу3x3 массива в приращении.
(=B14-B13);( =C14-C13):( =D14-D13)
(=B19-B13);( =C19-C13);( =D19-D13)
(=B16-B13);( =C16-C13);( =D16-D13)
=G14-G13; =-(H14-H13); =I14-I13; =J14-J13; =K14-K13; =L14-L13; =M14-M1;
=G19-G13; =-(H19-H13); =I19-I13; =J19-J13; =K19-K13; =L19-L13; =M19-M13;
=G16-G13; =-(H16-H13); =I16-I13; =J16-J13; =K16-K13; =L16-L13; =M16-M13;
Из полученных данных составляем матрицу нагрузок dPM:
=B22; =B23; =B24;
=C22; =C23; =C24;
=D22; =D23; =D24;
Составляем матрицу смещений SM:
=G22; =G23; =G24;
=H22; =H23; =H24;
=I22; =I23; =I24;
Вычисляем определитель матрицы смещений SM:
=F27*G28*H29+F28*G29*H27+F29*G27*H28-F29*G28*H27-G27*H29*F28-F27*G29*H2
Обратная матрица SM-1:
=(G28*H29-G29*H28)/J28; =-(G27*H29-G29*H27)/J28; =(H28*G27-H27*G28)/J28;
=-(F28*H29-F29*H28)/J28; =(F27*H29-F29*H27)/J28; =-(F27*H28-F28*H27)/J28;
=(F28*G29-F29*G28)/J28; =-(F27*G29-F29*G27)/J28; =(F27*G28-F28*G27)/J28;
Составляем матрицу жесткости С:
=B27*L27+C27*L28+D27*L29; =B27*M27+C27*M28+D27*V28; =B27*N27+C27*N28+D27*N29;
=B28*L27+C28*L28+D28*L29; =B28*M27+C28*M28+D28*M29; =B29*N27+C29*N28+D29*N29;
=B28*N27+C28*N28+D28*N29; =B29*M27+C29*M28+D29*M29; =B29*N27+C29*N28+D29*N29;
Проверка преобразований:
=C31*F27+D31*F28+E31*F29;
=C32*G27+D32*G28+E32*G29;
=C33*H27+D33*H28+E33*H29.
Расчет окончен
ВЫВОДЫ
1.В результате проделанной работы был разработан нагрузочный стенд. Что привело к более точной оценки показателей упругости рабочих органов почвообрабатывающих машин, благодаря возможности прикладывать нагрузку по трем различным направлениям.
В нагрузочном стенде были разработаны: столик для проведения замеров координат трех точек лапы под нагрузкой. С возможностью регулирования горизонтальности, при помощи подвесов.
Шарнирная опора, имеющая возможность перемещаться вдоль рамы по средствам винтового механизма, для обеспечения соосности центров отверстий в стойке и самой опоре. Так же возможно вращение опоры для приложения нагрузки под различными направлениями.
Поворотная консоль, соединяемая с шарнирной опорой по средствам трубы, и имеющая возможность перемещаться в поперечном направлении для приложения нагрузки под разными направлениями.
2. Результаты исследования показывают, что на кинематику действует ряд факторов. Так, управлять эффективно величиной l можно отнесением носка рабочего органа Т и в меньшей степени конфигурацией стойки. Чем больше конфигурация отнесена назад, тем ближе режим выглубления.
- Угловые искажения зависят главным образом от жесткости крепления и конфигурации упругого контура. Уменьшать жёсткость, не снижая прочности, можно увеличением длины стойки, завивая её витками в заданный габарит.
Бутовченко А.В., Игнотенко И.В., Рулевский А.М. Донской государственный технический университет, г. Ростов-на-Дону, РФ
УДК 631.31 ГРНТИ 55.57.31
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
- 1. Багиров И.3. Исследование деформации и сопротивления грунта при взаимодействии с клином на высоких скоростях - Минск, 1963.
- Базаров В.П. Зависимость тягового сопротивления культиватора КПЭ-3,8 от числа пружин подвески // Механизация и электрификация сельского хозяйства. 1983. №5.
- Бугайченко Н.В. Обоснование параметров полольных лап культиваторов для работы на повышенных скоростях в зонах недостаточного увлажнения : Киев, 1964. - 22 с.
- Вайнштейн II.А., Вакман Д.Е. Разделение частот в теории колебаний и волн. - М.: Наука, 1983. - 288 с.
- Васильковский С.М. Сопротивление почв движению культиваторной лапы // Техника в сельском хозяйстве. 1996. №3. – С.17-19.
- Вилде А.А. Исследование работы, тягового сопротивления и изыскание рациональной конструкции рабочих органов культиваторов и пружинных борон // Тр. Латвийского НИИПТИМЭСХ. - Рига, 1972. Т.1V. - С.3-53.
- Вилде А.А., Цесниекс А.X. Исследование работы тягового сопротивления пружинных шлейф-борон // Тр. Латвийского НИИПТИМЭСХ. - Рига. 1974. Т.V11. - С.72-84.
- Вилде А.А. К вопросу резания грунта клином // Механизация и электрификация сельского хозяйства: Тр. Латв. НИИПТИМЭСХ. - Рига : Звайгзне, 1976. Вып.Х1(1Х). - С.115-127.
- Виноградов В.И., Бондарь С.А. Упрощенное рассмотрение взаимодействия корпуса плуга на упругой подвеске с почвенным пластом // Тр. ЧИМЭСХ. 1978. Вып.137. - С.53-59.
- Гасилин В.И., Игнатенко И.В. Упругая кинематика пружинных стоек культиватора // Динамика узлов и агрегатов сельхозмашин: сб. статей / РИСХМ. - Ростов н/Д, 1979. - С.109-113.
- Горячкин В.П. Земледельческая механика. – М.: Колос, 1919
- Дьяченко Г.Н. Основы теории перемещения клина в сыпучей среде // Проектирование рабочих органов почвообрабатывающих машин и зерноуборочной техники: Сб. статей / РИСХМ. - Ростов н/Д, 1985. - С.21-35.







.JPG)
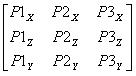


.JPG)
Оставить комментарий
Для того, чтобы оставить комментарий,
зарегистрируйтесь или войдите